Resistances In Parallel:

Whenever resistances are placed in parallel, they behave in a different way than they do in series. In common, when you have a resistor of a certain value and you put other resistors in parallel with it, and then overall resistance reduces. Mathematically, the rule is clear-cut, though it can get a little messy.

The one way to compute resistances in parallel is to consider them as conductances rather. Conductance is measured in units termed siemens, sometimes represented as S. (The term siemens serves both in the singular and the plural sense). In older documents, the term mho (ohm spelled backwards) is used rather. In parallel, conductances add up in similar way as resistances add in series. When you change all the ohmic values to siemens, you can add these figures up and convert the final answer back to ohms.

The symbol for conductance is G. Conductance in siemens is the reciprocal of resistance in ohms. This can be expressed tidily in the following two formulas. It is supposed that neither R nor G is ever equivalent to zero:

G = 1/R

R = 1/G

PROBLEM:

Consider five resistors in parallel. Name them R₁ through R₅, and call the total resistance R, as shown in the diagram below. Let R₁ = 100 ohms, R₂ = 200 ohms, R₃ = 300 ohms, R₄ = 400 ohms, and R₅ = 500 ohms, respectively. Determine total resistance R of this parallel combination?

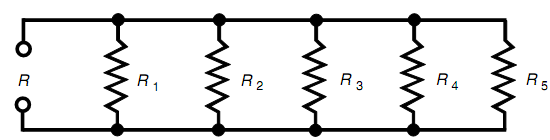
SOLUTION:

Altering the resistances to conductance values, you acquire G₁ = 1/100 =0.0100 siemens, G₂ = 1/200 = 0.00500 siemens, G₃ = 1/300 = 0.00333 siemens, G₄ = 1/400 = 0.00250 siemens, and G₅ = 1/500 = 0.00200 siemens. Adding these, G = 0.0100 + 0.00500 +0.00333 +0.00250 + 0.00200 = 0.02283 siemens. The total resistance is thus, R = 1/G =1/0.02283 = 43.80 ohms. Since we are given that the input numbers to only three significant figures, we must round this off to 43.8 ohms.

Whenever you have resistances in parallel and their values are all equivalent, the total resistance is equivalent to the resistance of any one component divided by the total number of components. In a more common sense, the resistances shown in figure combine like this:

R = 1/ (1/R₁+ 1/R₂ + 1/R₃ + 1/R₄ +     1/R₅)

When you prefer to use exponents, the formula appears like this:

R = (R₁^-1 + R₂^-1 + R₃^-1 + R₄^-1 + R₅^-1)

Such resistance formulas are cumbersome for several people to work with, though mathematically they symbolize the similar thing we just did.