Kirchhoff's Voltage Law:

The total sum of all the voltages, as you go about a circuit from a fixed point and return there from the reverse direction, and taking polarity into account, is always zero. In first thought, some people find this strange. Certainly there is voltage in your radio, electric hair dryer, or computer! Yes, there is-among various points in the circuit. Though, no single point can have an electrical potential with respect to itself. This is too easy that it is trivial. A point in a circuit is forever shorted out to itself.

What Kirchhoff was saying whenever he wrote his voltage law is that voltage cannot emerge out of nowhere, nor can it disappear. All the potential differences should balance out in any circuit, no matter how complex and no matter how many branches there are.

Consider the rule you have already learned about series circuits: The voltages across all the resistors add up to the supply voltage. Though, the polarities of the emfs across the resistors are opposite to that of the battery. This is shown in figure. It is a subtle thing, though it becomes clear whenever a series circuit is drawn with all the components, involving the battery or other emf source, in line with each other, as in figure below.

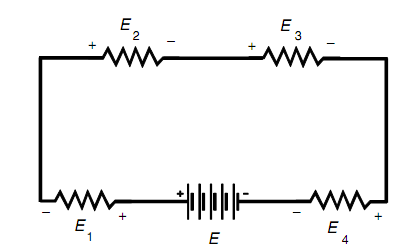
Figure: Kirchhoff's voltage law. The sum of the voltages E + E₁ + E₂ + E₃ + E₄ = 0, taking polarity into account.

PROBLEM:

Refer to the diagram as shown below. Assume that the four resistors have values of 50, 60, 70, and 80 ohms and that the current through all them is 500 mA (i.e., 0.500 A). Compute the supply voltage E?

SOLUTION:

Find the voltages E₁, E₂, E₃, and E₄ across each of the resistors. This is completed by using Ohm's law. In the situation of E₁, say, with the 50-ohm resistor,

E₁ = 0.500 x 50 = 25 V. In similar way, you can compute E₂ = 30 V, E₃ = 35 V, and E₄ = 40 V. The supply voltage is the sum E₁ + E₂ + E₃ +  E₄ = 25 + 30   + 35 +  40 V = 130 V.