Kirchhoff's Current Law:

Kirchhoff stated that current should work something like water in a network of pipes and that the current leaving into any point has to be similar as the current going out. This is correct for any point in a circuit, no matter how many branches go ahead into or out of the point (The figure is as shown below).

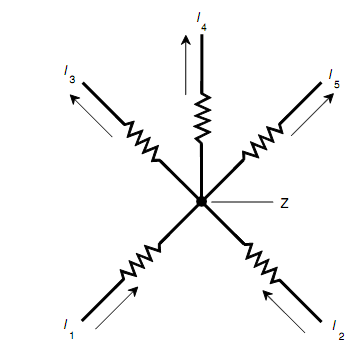
Figure: Kirchhoff's current law.

The current entering point Z is equivalent to the current leaving point Z. In this situation, I₁ + I₂ = I₃ + I₄ + I₅.

In a network of water pipes which does not leak and into which no water is added all along the way, the total number of cubic meters leaving in has to be similar as the whole volume leaving out. Water cannot form from nothing, nor can it vanish, within a closed system of pipes. Charge carriers, consider Kirchhoff, should act the similar way in an electric circuit.

PROBLEM:

In figure shown below, assume that each of the two resistors below point Z has a value of 100 ohms and that all three resistors above Z contain values of 10.0 ohms. The current via each 100 ohm resistor is 500 mA (i.e., 0.500 A). Compute the current through any of the 10.0 ohm resistors, assuming that the current is equally distributed? Determine the voltage, then, across anyone of the 10.0 ohm resistors?

SOLUTION:

The total current into Z is 500 mA + 500 mA = 1.00 A. This should be divided into three ways uniformly among the 10 ohm resistors. Hence, the current through any one of them is 1.00/3 A = 0.333 A = 333 mA. The voltage across any one of the 10.0 ohm resistors is found by using Ohm's law: E = IR = 0.333 x 10.0 = 3.33 V.