Reaction Function Approach:

The reaction function approach is a useful tool in analysing oligopolistic markets. With this approach, it becomes easier to analyse the equilibrium condition of the different oligopolistic models. We would apply it to the Cournot duopoly model in the following.

In his duopoly model, Cournot makes a very naïve assumption that the firms think their rivals would stick to their past periods output level. Therefore, the conjectural variation (CV) of both the duopolists is equal to zero. Retaining the same assumptions that both the duopolists i) face linear market demand curve, ii) maximise profit and iii) have MC = 0.We can write the model as follows:
Let the demand function be p = a - bq, where q = (qi + qj) = total market demand and a, b > 0

Given the above assumptions, we can write the profit function of the i^th firm as:
       Π_i = pq_i - C (q_i); where i = A, B              
            = (a - bq) q_i  - C(q_i)     
            = [a - b(q_i + q_j) ] q_i  - C(q_i)   
Each firm being a profit maximiser, we would differentiate Π_i partially with respect to qi and set the derivatives equal to zero.  

Thus, δΠ_i/ δq_i = a - 2bq_i -b (q_j + q_i δq_j/δq_i) - δC/ δq_i  = 0.

As in this model CV = 0, δqj/δqi = 0. Hence, we have, a - 2bq_i -bq_j = 0    (as δC/ δq_i = 0, by assumption)
From such an optimisation exercise we get:

q_i* =  (a - bq_j)  / 2b, q_i*  = R_i (q_j) where, qi* gives the profit maximising level of output of firm i(i, j =A, B; i ≠j)

The equilibrium output levels of both the firms is obtained by solving the two reaction function equations as:

       q_A* = a/3b, q_B* = a/3b

For each firm, Ri represents the reaction function. Given the output level of the jth firm the reaction function shows the best response (i.e., qi*) of the i^th firm, which maximises its profit. The reaction functions in this exposition will be downward sloping straight lines, as shown below in Figure where SP is the reaction function of firm B and MN is the reaction function of firm A.

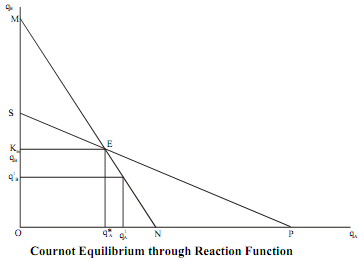
For any level of output of firm B say ₁qB¹ the level of output which would maximise firm A's profit is given by qA₁ from A's reaction function MN .We can similarly explain each point on the reaction curve of firm B.