Error Variance Varies Directly with an Independent Variable:

The most commonly used assumption is that σ²  is associated with a variable. If the variance of the ithobservation  is proportional to the square of the explanatory variable, then deflation  by this variable  results  in a model exhibiting  homoscedasticity. Suppose the variance of the  iIh  observation is proportional  to  the square of the explanatory variable, X. Thus  

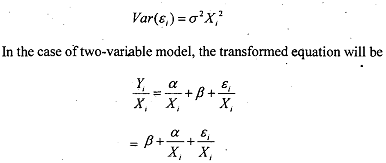
Hence, the variance of  the disturbance  term is now constant, and we can proceed  to apply OLS to the transformed equation (8.12), by  regressing 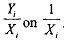. In our original  regression model a  is  the intercept and β is  the slope parameter. In the transformed regression model,  however, Q  is the intercept and a  is the slope. Therefore,  to get back the original model we need to multiply the estimated transformed model by X. Notice that by applying OLS method to (8.12) we obtain estimators which are BLUE.