Non-iterative Methods of Obtaining ρ:

A couple of simple methods of obtaining a crude estimate of p are as follows:

Using the Durbin- Watson  statistic: Since d has been estimated earlier while conducting  the test, and we know  that as  the sample gets large that is as T+w, this statistic tends to 2(1-p). We  can use this fact to construct the estimator:

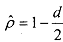
Note that this estimator is only good for very large samples and in small samples this gives highly inaccurate results and should be avoided. From residuals :  Ifthe AR(1)  scheme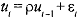,is  true, then p  can be obtained easily by running a regression of the residuals u, on u_t-1.  That is,

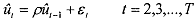
Nolethat the equation (2)  does not have  a constant. The estimate of p obtained  is consistent since the zi, are consistent estimators of the true u,.  Again, this estimate can be used in the transformation to obtain the BLUE estimates of β₁, and β₂  respectively, after applying the Cochrane-Drcutt transformatioil given at (2).

Durbin  's Method: One can rearrange by moving  the Y_t-1, term to the right hand side, so  that

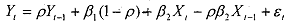
and running OLS on instead. Note that no prior estimate of p  is required here. The error in 3 is classical, and we can show that the estimate of p obtained as the coefficient of  Y_t-1,  in this case is biased but consistent. This is the Durbin estimate  of p₀ let us call it p₀.  Next, the seeond step  of  the Cochrane- Orcutt procedure is performed by using this estimate of p.  That is, we estimate the regression by using this &,  to get the estimates of β₁, and β_2.