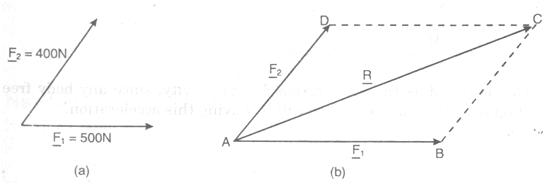
Law of Parallelogram of Forces:

If the two coplanar forces meet at a specific point, their resultant can be found by the law of parallelogram of forces, which states that, "If two of forces working at a point are such that they may be represented in magnitude and direction by two adjacent sides of parallelogram, the diagonal of the parallelogram passing out through their point of intersection gives the resultant in magnitude and direction".

Let two forces P and Q working at point O in a given body as illustrated in Figure (a). Their combined effect may be found out by constructing a parallelogram by using vector P and vector Q as two adjacent sides of the parallelogram as illustrated in Figure (b). The diagonal passing out through O represents their resultant in magnitude and direction. You may prove through the geometry of the figure that the magnitude R of the resultant and the angle it makes with P are given by :

tan θ = Q sin α / (P + Q cos α)     or tan β = P sin α / (Q + P cos α)

where,  α is the angle among P¯ and Q¯ .

θ is the angle among R¯ and P¯ .

β is the angle among R¯ and Q¯ .

The above two forces may also be combined using the law of triangle of forces that states that if the second force is drawn from the end of the first force (taking care of direction and magnitude), after that the line joining the beginning point of first force to the end of the second force represents their resultant.

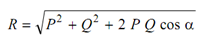
sin θ = (Q/ R ) sin α,

sin β =( P/ R) sin α