Moment of a Force:

If a force F is working on a body, resting at O, and the line of action of this force does not pass through G, the centre of gravity of the body, it shall not impart the body a straight line motion, called as the translatory motion, but shall try to rotate (turn) the body around O as illustrated in Figure. The measure of this property of force through virtue of that it tends to rotate the body on which it acts is called as the moment of a force. The rotation of the body can be either about a point or a line.

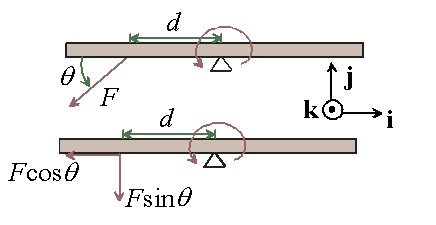
Referring the Figure, if F is the force (in N) working on the body along with the line AB, and x is the perpendicular distance (in m) of O (say, a pin that holds the body) from AB, after that

Moment of the force F around O, M = F × x = F × OC

Here, point O is called as moment centre or fulcrum, and distance x is termed as moment arm.