Partially Bi-cubically Blended:

The bilinearly blended Coons patch solves out a problem of considerable importance with very little effort, however we pay for that by an annoying drawback. Let Figure: It illustrated two bilinearly blended Coons patches, explained over u ∈ [0, 2], v ∈ [0, 1]. The boundary curves v = 0 and v = 1, both composite curves, are differentiable. Though, the cross boundary derivative is obviously discontinuous along u = 1.

Analyzing this difficulty, we see that it may be blamed on the fact that cross boundary tangents along with one boundary based on data not pertaining to that boundary. For instance, for any given bilinearly blended Coons patch, a change in the boundary curve p(1, v) shall affect the derivatives across the boundary p(0, v).

We may separate the derivatives across one boundary from information along with the opposite boundary by utilizing different blending functions, say some that have zero slopes at the endpoints. Striving for simplicity, we may find two for such blending functions: the cubic Hermite polynomials 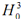and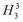.