Coons Patches:

Now we are ready to create a Coons patch x. It is given by

                            x = r_c + r_d - r_cd

or, in the form of a recipe: "loft_u + loft_v - bilinear". The concerned surfaces and the solution are shown in Figure. Writing in full detail gives

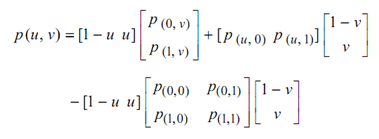
Now we can justify the name "bilinearly blended" for the above Coons patch: a ruled surface "blends" together the two defining boundary curves; this blending occurs in both directions. Though, the Coons patch is not normally itself a bilinear surface - the name refers purely to the method of construction.

The functions 1 - u, u and 1 - v, v are called as blending functions. A close inspection of 5.40 reveals that several other pairs of blending functions, say, f₁ (u), f₂ (u) and g₁ (v), g₂ (v), could also be utilized to construct a generalized Coons patch. Then it would be of the general form

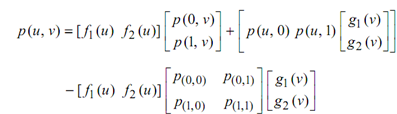
Figure: Coons Patches : A Bilinearly Blended Coons Patch is Composed of Two Lofted Surfaces and a Bilinear Surface

There are just two limitation on the f_i and g_i : each pair should sum to one identically : or else we would produced non-barycentric combinations of points. Also, we should have f₁ (0) = g₁ (0) = 1, f₁ (1) = g₁ (1) = 0 in fact interpolate. The shape of the blending functions contains a predictable effect on the shape of the resulting Coons patch. In general, one requires f₁ and g₁ to be monotonically reducing; this generated surfaces of predictable shape, but is not essential for theoretical reasons. Surface modellers which employ Coons patches typically permit designers to change the blending functions like a way to model the interior of the patch.