Bicubically Blended Coons Patch:

Cubic Hermite interpolation needs more input than positional data - first derivative information is required. Since our positional input consists of entire curves, not just points, the clear data to supply are derivatives along with those input curves. Now our given data consist of

p(u, 0), p(u, 1), p(0, v), p(l, v) and p_v(u, 0), p_v(u, 1), p_u(0, v), p_u(l, v)

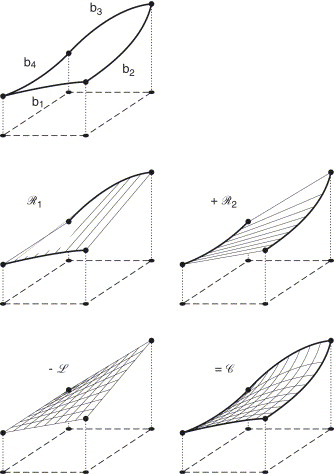
Figure: Coons Patches : for the Bicubically Blended Case, the Concept of the Lofted Surface is Generalized. In Addition to the given Boundary Curves, Cross Boundary Derivatives are Supplied

We may think of the now prescribed cross boundary derivatives as "tangent ribbons," shown in Figure (only two of the four "ribbons" are illustrated there).

The tensor product of bicubic Hermite interpolant is :

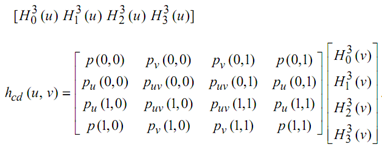
The bicubically blended Coons patch now becomes

p = h_c + h_d - h_cd

Before closing this section, we have to take a closer look at the h_cd part of eq.

On closer inspection, we determine that it wants data that we were not desire to provide in our initial problem description, say, the central "twist partition" of the 4 × 4 matrix in Eq. The bicubically blended Coons patch needs these quantities as input, and it has caused CAD software developers several headaches as Coons proposed his surface scheme in the year 1964. The most popular "solution" appear to be simply to describe each of the four corner twists to be the zero vector.