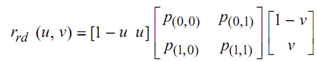Bi-linearly Blended Coons Patch:

A ruled surface interpolates to two boundary curves - a rectangular surface, though, has four boundary curves, and that is exactly to what a Coons patch interpolates. This first instance of Coons patches was also developed first by Coons.

To be more accurate: given are four arbitrary curves c₁ (u), c₂ (u) and d₁ (v), d₂ (v), indicated over u ∈ [0, 1] and v ∈ [0, 1], respectively. Determine a surface x that has these four curves as boundary curves:

p(u, 0) = c₁ (u),  p(u, 1) = c₂ (u)

p(0, v) = d₁ (v),   p(1, v) = d₂ (v)

We have just built up ruled surfaces, so let us used them for this new problem.

The four boundary curves indicated two ruled surfaces :

                      r_c(u, v) = (1 - v) × (u, 0) + v × (u, 1)

and                   r_d(u, v) = (1 - u) × (0, v) + u × (1, v)

Both interpolants are illustrated in Figure, and we see that r_c interpolates to the c-curves, still fails to reproduce the d-curves. The situation for r_d is similar, and, so, equally unsatisfactory. Both r_c and r_d do well on two sides, still fail on

the other two, where they are linear. Our strategy is, thus, as follows: let s try to achieved what each ruled surface interpolates to and let us attempt to eliminate what it fails to interpolate to. A little thought reveals that the "interpolation failures" are captured by one surface: the bilinear interpolant r_cd to the four corners: