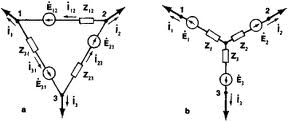
From the Delta Connection:

Resistance among terminals 1 and 2 whereas 3 is open circuited.

R_c and R_b are in series. This combination is in parallel to R_a.

R₁₂ =  R_a (R_b + R_c ) / R_a  + R_b + R_c

Figure 4.51

Likewise, the resistances between terminals 2 and 3 and 1 and 3 are given by :

R₂₃= (R_a  + R_c ) R_b/ R_a  + R_b + R_c      

R₁₃ = (R_a  + R_b ) R_c / R_a  + R_b + R_c

Now compare the results of star and delta connections:

R ₁ + R₂ = Ra (R_b + R_c )/ R_a  + R_b + R_c

R ₂  + R₃  =  R_b (R_a  + R_c )/ R_a  + R_b + R_c

R ₁ + R₃ = Rc (R_a + R_b )/ R_a + R_b + R_c

We may determine three unknown resistances R_a, R_b and R_c in terms of R₁, R₂ and R₃.

R _a   = R₁ R₂ + R₂ R₃ + R₃ R₁/ R₃

R _b   = R₁ R₂ + R₂ R₃ + R₃ R₁/ R₁

R _c  = R₁ R₂ + R₂ R₃ + R₃ R₁ / R₂