Overall Heat Transfer Coefficient

Most of the heat transfer procedures encountered in nuclear facilities include a combination of both conduction and convection. For illustration, the heat transfer in a steam generator includes convection from the vastness of the reactor coolant to the steam generator internal tube surface, conduction via the tube wall, and convection from the external tube surface to the secondary side fluid.

In situations of combined heat transfer for a heat exchanger, there are two values for h. There is the convective heat transfer coefficient (h) for the fluid film within the tubes and a convective heat transfer coefficient for the fluid film exterior the tubes. The thermal conductivity (k) and thickness (Δx) of the tube wall should also be accounted for. An additional term (U_o), termed as the overall heat transfer coefficient, should be used rather. It is general practice to associate the total rate of heat transfer (A_o ) to the cross-sectional area for heat transfer (A_o) and the whole heat transfer coefficient (U_o). The association of the whole heat transfer coefficient to the separate conduction and convection words is shown in figure below.

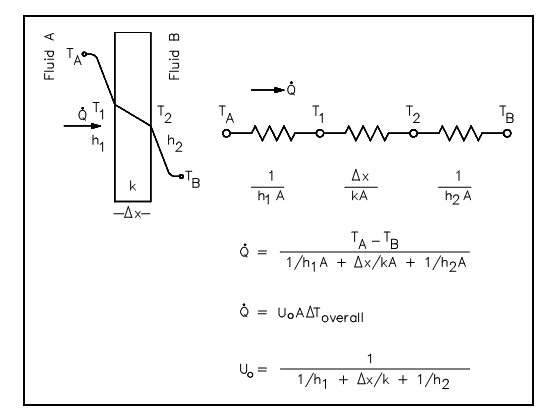
Figure: Overall Heat Transfer Coefficient

Remembering the equation:

Q = U_oA_oΔT_o

Here:

U_o is stated in the figure shown above.

The illustration of this concept exerted to the cylindrical geometry is shown by the figure below that illustrates a usual combined heat transfer condition.

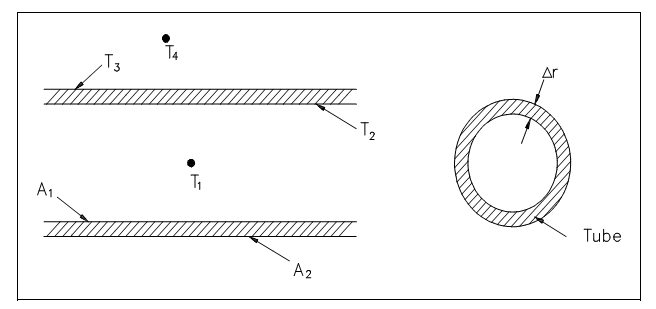
Figure: Combined Heat Transfer

By using the figure symbolizing flow in a pipe, heat transfer by convection takes place among temperatures T₁ and T₂; the heat transfer by conduction takes place among temperatures T₂ and T₃; and heat transfer takes place by convection among temperatures T₃ and T₄. Therefore, there are three procedures included. Each has a related heat transfer coefficient, cross-sectional area for heat transfer, and temperature difference. The fundamental associations for these three procedures can be stated by using the equations.

Q = h1A1(T₁- T₂)

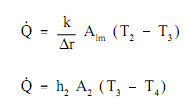
ΔT_o can be stated as the total of the ΔT of the three individual procedures.

ΔT_o = (T₁ - T₂) (T₂ - T₃) (T₃ - T₄)

When the fundamental association for each procedure is resolved for its related temperature difference and replaced into the expression for ΔT_o above, the association below outcomes.

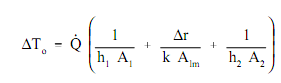
This association can be altered by chosen a reference cross-sectional area A_o.

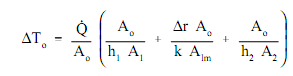
Resolving for outcomes in an equation in the form. Q - U_o A_o ΔT_o

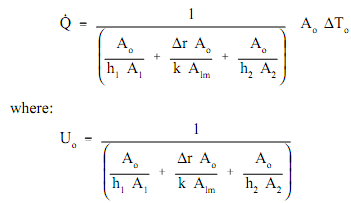
The above equation for the overall heat transfer coefficient in cylindrical geometry is associatively hard to work with. The equation can be simplify without losing much correctness when the tube which is being examined is thin-walled, which is the tube wall thickness is small as compared to the tube diameter. For a thin-walled tube, the internal surface region (A₁), external surface region (A₂), and log mean surface area (A_1m), are all very close to being equivalent. Supposing that A₁,A₂, and A_1m are equivalent to each other and also equivalent to A_o permits us to cancel out all the region terms in the denominator of the below equation.

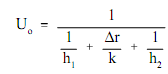
These outcomes in a much simpler expression which is alike to the one developed for a flat plate heat exchanger is shown in the figure above.

The convection heat transfer procedure is powerfully dependent upon the properties of the fluid being considered. Likewise, the convective heat transfer coefficient (h), the whole coefficient (U_o), and the other fluid properties might differ substantially for the fluid when it experiences a great temperature change during its path via the convective heat transfer device. This is particularly true when the fluid's properties are powerfully temperature dependent. Under such situations, the temperature at which the properties are "looked-up" should be some kind of average value, instead of using either the inlet or outlet temperature value.

For inner flow, the bulk or average value of temperature is acquired analytically via the use of conservation of energy. For exterior flow, an average film temperature is generally computed, that is an average of the free stream temperature and the solid surface temperature. In any situation, an average value of temperature is used to acquire the fluid properties to be employed in the heat transfer trouble.