Support Reactions:

To find the support reaction we consider the free body diagrams of each beam span as shown below :

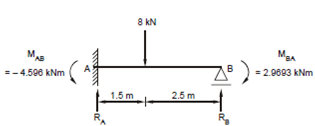
(a) Free Body Diagram of AB

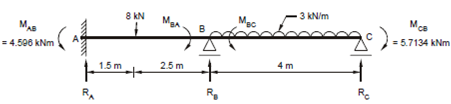
(b) Free Body Diagram of ABC

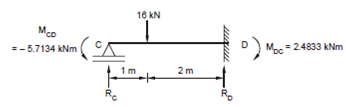
(c) Free Body Diagram of CD

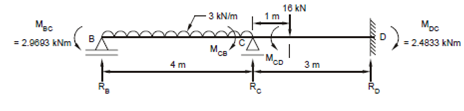
(d) Free Body Diagram of BCD

Figure: Free Body Diagrams

(a) Considering free body diagram of AB, shown in Figure (a), it is acted upon by a anticlockwise couple of - 4.5960 at end A, and + 2.9693 kNm at end B; while a load of 8 kN is acting downwords at point 1.5 m to right of A. Let the support reactions at A and B be R_A and R_B.

Taking moments about end B, we have,

- 4.596 - 8 × 2.5 + R_A × 4 + 2.9693 = 0

giving R_A = 5.4066 kN

(b) Next considering the free body diagram of the two spans ABC shown in Figure (b) the end couples are M_AB = - 4.596 kNm and M_BC = + 5.7134 kNm. The moment M_BA and M_BC at the intermediate support B cancel out each other as they are equal in magnitude but opposite in sign. The concentrate load of 8 kN is acting in span AB and a uniformly distributed load of 3 kN/m over span BC. The support reaction at A, B, C is R_A, R_B, R_C of which R_A is known to be 5.4066 kN.

∴ Taking moment of all forces about point C, we have

- 4.5960 + 5.7134  - 8 × 6.5 - (3 × 4) × 2 + 5.4066 × 8 + R_B × 4 = 0

giving R_B  = 7.9076 kN         . . . (ii)

(c) Similarly, from free body of CD, shown in Figure 9(c), we get the equation (taking moment about point C)

- 5.7134 + 2.4833 + 16 × 1 - R_D × 3 = 0

giving R_D = 4.2564 kN

Again from free body of BCD shown in Figure (d), taking moments about B, we get,

- 2.9693 + 2.4833 + (3 × 4) × 2 + 16 × 5

- R_C × 4 - 4.2566 × 7 = 0

giving R_C = 18.4294

Thus, the four support reaction is as follows:

R_A = 5.4066 kN

R_B = 7.9076 kN

R_C = 18.4294 kN

R_D = 4.2564 kN

The sum of all these reaction is 36 kN which is the same as the total downward load, i.e. 8 + 3 × 4 + 16 = 36 kN.