Support Reactions:

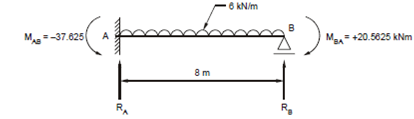
From Free Body Diagram of AB shown in Figure 12(a), taking moments about B,

- 37.625 + 20.5625 - (6 × 8) × 4 + R_A × 8 = 0

giving R_A = 26.133 kN

(a) Free Body Diagram of AB

(b) Free Body Diagram of BC

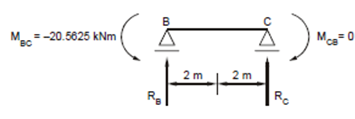
(ii)       To Free Body Diagram of BC shown in Figure 12(b).

Taking moments about B

- 20.5625 + 16 × 2 - R_C × 4 = 0

giving R_C = 2.859 kN.

Further considering vertical equilibrium of the structure

R_A + R_B + R_C = 6 × 8 + 16 = 64

Substituting the values 26.133 + R_B + 2.859 = 64

giving R_B = 35.008 kN.

Now, the Bending Moment Diagram (BMD) and Shear Force Diagram (SFD) can be drawn as shown in Figure 13.

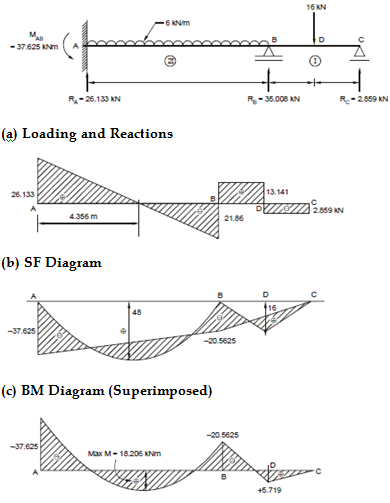
Note: Show that the maximum positive BM in the span AB occurs at 4.356 m from A and its value is 18.906 kNm. Also find the position of points of contraflexure (BM = 0).