Relationship between depth and pressure

Someone who dives beneath the surface of the water observes that the pressure on his eardrums at a depth of even some feet is observably more than atmospheric pressure. Cautious measurements illustrate that the pressure of a liquid is directly proportional to the depth, and for a specified depth the liquid applies the similar pressure in all directions.

As shown in figure below the pressure at various levels in the tank differs and this causes the fluid to leave the tank at different velocities. The pressure is defined to be force per unit area. In the situation of this tank, the force due to the weight of the water over the point where the pressure is being established.

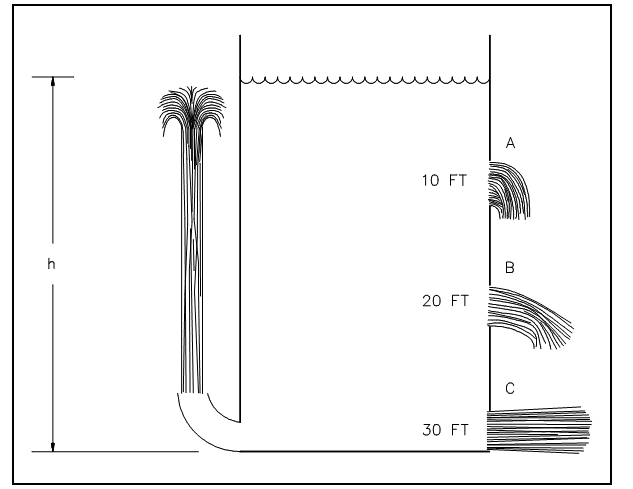
Figure: Pressure versus Depth

Example:

Here:

m = mass in lbm

g = acceleration due to earth's gravity i.e., 32.17ft/sec²

g_c = 32.17 (lbm ft)/ (lbf sec²)

A = area in ft²

V = volume in ft³

ρ = density of fluid in lbm/ft³

The volume is equivalent to the cross-sectional area time the height (h) of liquid. Replacing this in to the above equation outcomes:

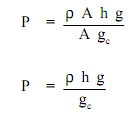
This equation tells us that the pressure applied by a column of water is directly proportional to the height of the column and the density of the water and is independent of the cross-sectional area of the column. The pressure thirty feet beneath the surface of a one inch diameter standpipe is the similar as the pressure thirty feet beneath the surface of a large lake.