Measurement Errors in both X and Y:

Now let us assume that both X  and Y have errors of measurement. The true model is as before

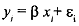
Since  X and Y have errors of measurement, we observe x* and y* instead of x_i and y_i, such that A,  .

where u_i and v_i present the errors  in  the values ofyl  and x,  respectively. We make the following assumptions about the error terms:

(i) There is no correlation between the error  term and corresponding variable,  i.e.,

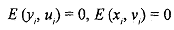
(i)  There  is  no correlation between error of one variable and measurement of  the other variable, i.e,,

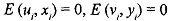
i) There is  no correlation between errors in measurement of both the variables, i.e.,

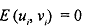
On the basis of the above assumptions, our estimated regression equation will be  

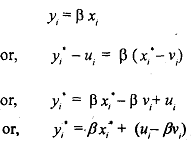
Equation (9.8) shows that if we model y* as a function of  x* the transformed disturbance contains measurement error in β. We then write  the OLS estimaton β' as

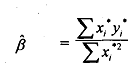
By substiuing the values of x*  and y*  in terms of x and y we find that

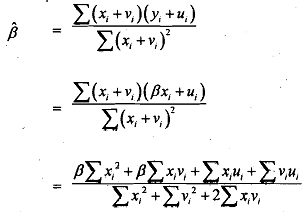
From above we observe  that E(β) ≠ β.

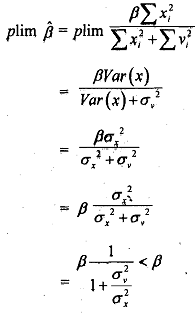
Thus, β' will not be a consistent estimator of β. The presence  of measurement error of the type in question will lead  to an underestimate  of  the  true  regressiortpararneter if ordinary least squares are used.