Measurement Error in Y:

Let us assume that only  the dependent variable contains error of measurement. Assume that the true regression model (written  in deviation form)  is

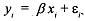
where E,  represents errors  associated with the specification of the model (the effects of omitted variables, etc.).

Assume that the variable y*,  instead.of  y, is obtained in the measurement process such that.

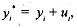
The measurement error u, is not associated with the regressor. Thus we have

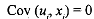
The  regression model  is  estimated with y' as  the dependent variable, with no account being taken of the fact that  y* is not an accurate measure  ofy. Therefore,  instead of estimating Eq. (9.  I), we estimate

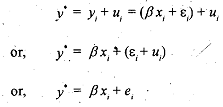
where e_i is a composite error term, containing the population disturbance  term ε, (which may be called the error term in the equation) and the measurement error term u_i.

For simplicity let us assume that 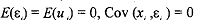(which is the assumption of classical linear regression), and Cov (x_i,  u_i) =  0, i.e., the errors of measurement in  yeare  uncorrelated with x_i, and Cov (ε_i, u_i) = 0,  th,e equation error and measurement error are uncorrelated. With these assumptions,  it can be shown that  P estimated  from  either  (9.1)  or (9.3) will be an unbiased estimator of the true P. Thus,  the errors of measurement in dependent variable  do not destroy  the unbiased property of  the OLS estimators. However, the variances and standard errors of  P estimated from (9.1)  and (9.3) will be different  because, employing the usual formula, we obtain

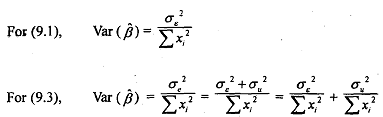
Obviously, the variance given at 19.5)  is larger than the variance given at (9.4). Therefore,  although  the errors  of measurement in  the dependent variable still give unbiased estimates af  the parameters and their variables, the estimated variances are now larger than the case where there are no such errors of measurement.