Measurement Error in X:

We have taken the true regression model deviation  form to be

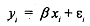
Now  let us assume that explanatory variable x, is measured with error and  the observed value becomes x,'  such  that  

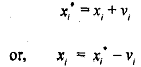
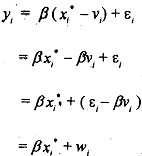
where 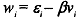   We  have assumed earlier that the measurement error in x is normally  distributed with  zero  mean, it  has  no serial  correlation, and it  is  uncorrelated with E,  . However, we  can no longer assume that the composite error term w, is independent of the explanatory variable x_i*  .

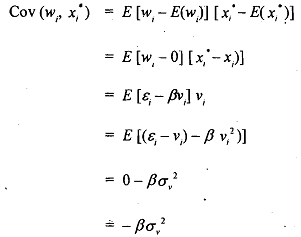
The composite error term w,  has mean zero as 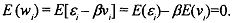Thus, the explanatory variable and  the error term are correlated, which violates the cpcial assumption of the classical linear regression model that  the explanatory variable is uncorrelated with the stochastic disturbance term. If this assumption  is violated, then OLS estimates are not only biased but also inconsistent;  they  remain biased asymptotically,  Let us now show this.

Instead of being able to estimate true relationship  (9.1), we are forced to replace x_i by  x_i*. Now the OLS estimator is

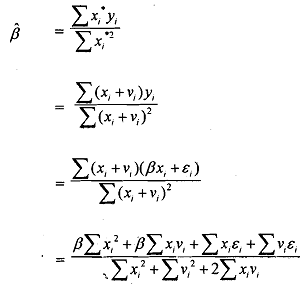
From above we find  that  β is a  biased estimate  as  E(β) ≠ β. Let us see  the asymptotic properties of β. Since v_i and q_i are stochastic and are uncorrelated with each other as well as with x,, we can say that

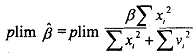
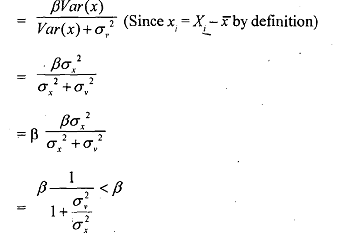
Thus, β' is biased even for an infinite sample  and β' is an  inconsistent estimator of β.