Equivalent Resistance Method

It is possible to compare heat transfer to the current flow in electrical circuits. The heat transfer rate might be considered as a current flow and the grouping of thermal conductivity, thickness of material, and region as a resistance to this flow. The temperature disparity is the potential or driving function for the heat flow, resulting in Fourier equation being writes in a form alike to Ohm's Law of Electrical Circuit Theory. When the thermal resistance term ?x/k is written as a resistance term where the resistance is the reciprocal of the thermal conductivity divided by the thickness of the material, the outcome is the conduction equation being equivalent to electrical systems or networks. The electrical analogy might be employed to solve complicated problems including both series and parallel thermal resistances. The student is termed to the figure shown below, illustrating the equal resistance circuit. A usual conduction trouble in its equivalent electrical form is given and the Fourier equation might be written as follows.

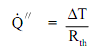
Here:

Q" = Heat Flux (Q/A) (Btu/hr-ft²)

ΔT = Temperature Difference (^oF)

R_th = Thermal Resistance (?x/k) (hr-ft²-^oF/Btu)

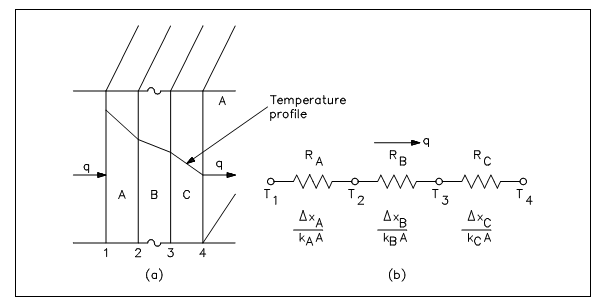
Figure: Equivalent Resistance