Conduction-Cylindrical Coordinates

The heat transfer across a rectangular solid is the most direct application of the Fourier's law. The heat transfer across a pipe or heat exchanger tube wall is more complex to compute. Across a cylindrical wall, the heat transfer surface area is repeatedly rising or reducing. The figure shown below is a cross-sectional view of a pipe built of a homogeneous material.

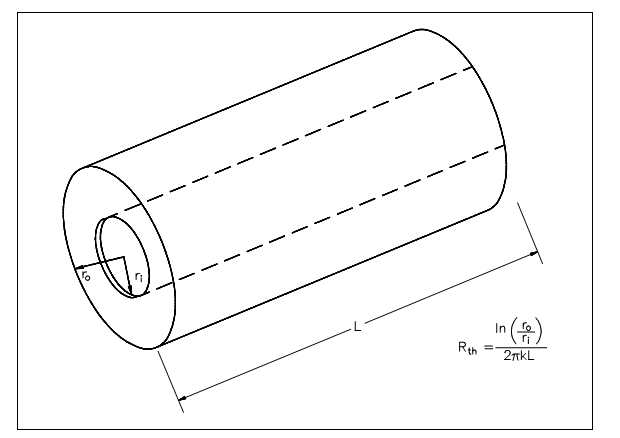
Figure: Cross-sectional Surface area of a Cylindrical Pipe

The surface area (A) for transferring heat via the pipe (i.e., neglecting the pipe ends) is directly proportional to the radius (r) of the pipe and the length (L) of the pipe.

A=2πrL

As the radius rises from the inner wall to the outer wall, the heat transfer area rises.

The development of an equation computing heat transfer via an object with cylindrical geometry starts with the Fourier's law equation as follows:

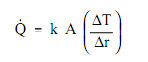
From the conversation above, it is view that no easy expression for region is accurate. Neither the region of the inner surface nor the region of the outer surface only can be employed in the equation. For a problem including cylindrical geometry, it is essential to state a log mean cross-sectional area (A_lm).

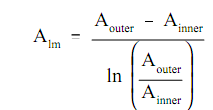
Replacing the expression 2πrL for area in the above equation permits the log mean area to be computed from the inner and outer radius without first computing the inner and outer region.

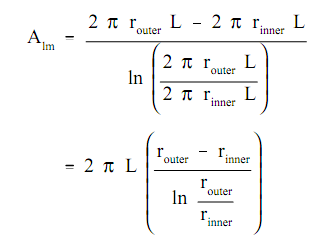
Such expression for log mean area can be inserted into the equation, permitting us to compute the heat transfer rate for cylindrical geometries.

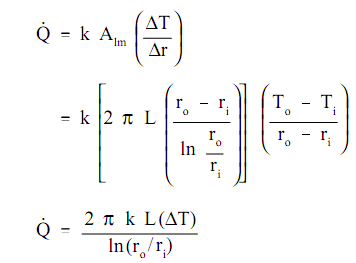
Here:

L = length of pipe (ft)

r_i = inside pipe radius (ft)

r_o = outside pipe radius (ft)

The computation of heat transfer via a cylindrical wall can be extended to involve a composite body composed of numerous concentric, cylindrical layers, as shown in figure below.

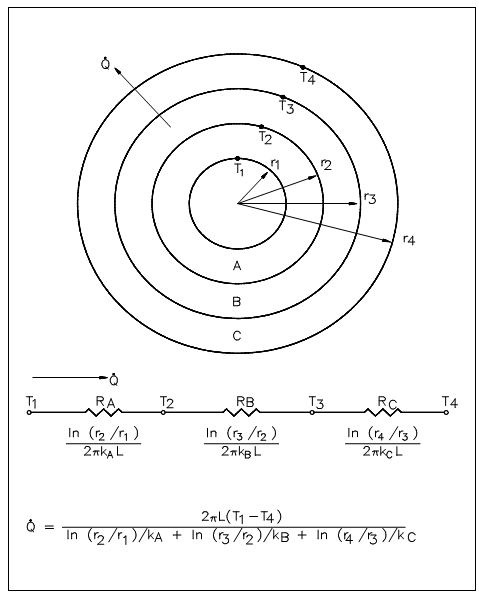
Figure: Composite Cylindrical Layers