Example of Propped Cantilever
A propped cantilever of span L carries a concentrated load P at a distance of a from the fixed support as shown in figure below. Find the support reactions and draw the BM and SF diagrams. Here EI is constant for the beam.
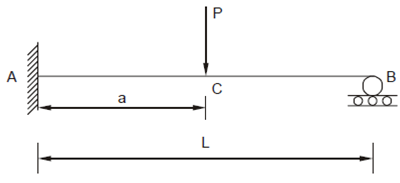
Solution
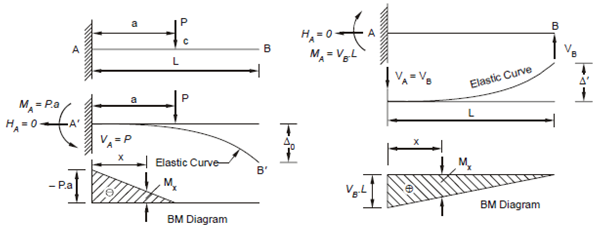
(a) Cantilever under External Load P (b) Cantilever with Reaction VB
The problem could be divided within two parts (which will be joined together later on).
(a) A cantilever fixed at A and free at B, acted upon by the load P. The reactions and bending moment diagram can be easily verified as given in Figure 4(a).
(b) The same cantilever acted upon by the unknown reaction VB acting at the end B. The reactions and the BM diagram are shown in Figure.
(i) To determine the downward deflection Δ0 due to the load P.
There are two regions :
In the region AC, where 0 ≤ x ≤ a .
M = - P (a - x)
In the region CB, where a ≤ x ≤ l .
M = 0
For the region AC, M = EI d2y/dx = - P (a - x) .
On integration the slope dy/dx = - P/EI (ax-x2/2)+A.
And deflection y= -P/EI(ax2/2-x3/6)+Ax+B.
The arbitrary constants could be found from the conditions:
Slope at A (x = 0) is zero and deflection at A (x = 0) is also zero which gives the value of the arbitrary constants A = 0 and B = 0.
∴ Between A and C,
Slope dy/dx = - P/EI (ax-x2/2)
Deflection y= -P/EI(ax2/2-x3/6)
Again in the region CB,
M = 0 ⇒ EI d2y/dx2 =0
On integration
Slope, dy/dx =C
and Deflection, y = Cx + D
where C and D are arbitrary constants.
To search the arbitrary constants C and D we have the following conditions:
The slope and deflection at the common point C shall be same as determined by Eqs.
From First Set:
Slope at C
dy/dx = - P/EI (a2-a2/2)= -Pa2/2EI
Deflection at C
y = - P/EI(a3/2-a3/6)= -Pa3/3EI
From Second Set :
Slope at C
dy/dx=C
Deflection at C
Y=Ca+D
Equating the corresponding values, we will get
C = - Pa2/2 EI
Ca + D = - Pa3/3 EI
from that the value of the arbitrary constants are found to be
C = - Pa2/2 EI
D = + Pa3/6 EI
On substitution, the Eqs.
Slope dy/dx =- Pa2/2 EI
Deflection y=- Pa2x/2 EI+ Pa3/6 EI