Rectangular Section:

Consider the point of application of the load P have the coordinates (x, y), with reference to the axes illustrated in Figure (a) in which x is positive when measured to right of O and y is positive when measured upwards.

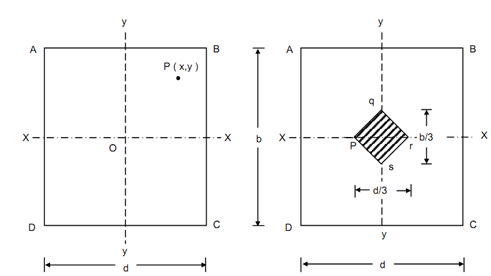
(a)                                                                       (b)

Figure

The stress at any point have coordinates (x′, y′) shall be

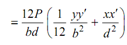
f  =  (P/ bd) + (P × yy′)/((1/12)db³) + P × xx′/((1/12)db³)

   =(12P/bd)((1/12)(yy′ /b²)+( xx′ /d²)

At D, have, x′ =- d/2 and y′ =- b/2  and, therefore, f will be minimum. Therefore, at D, we

                 f  = (6P/ bd) ((1/6) - (y/b) -  (x/d) )

The value of f reaches zero when

(y /b)+  (x/d) = 1   or  (6 y/b) +( 6x/d) = 1

Therefore, the deviation of the load line is governed by the straight line of Eq., whose intercepts on the axes are respectively b/6   & d/6. It is true for the load line is the first quadrant. Similar limits shall apply in other quadrants and the stress shall be wholly compressive during the section, if the line of action of P shall within the rhombus pqrs the diagonals of which are of length d /3 & b/3  , respectively. This rhombus is known the core of the rectangular section.