Strain Energy in Axial Loading:

Let the bar of length L & cross-sectional area A illustrated in given Figure to which an axial load P is applied. Under this load, the bar might extend or contract (extend if P is tension & contract if P is compression) by an amount Δ where the P - Δ relationship is a illustrated in Figure.

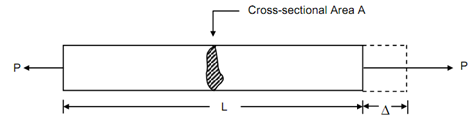
Figure

The work completed by the force P is equal to the strain energy stored in the bar.

Therefore,

U =( ½) P Δ

However, we know that the deformation, Δ = strain × L

Δ= (Stress/ E) × L = (P/ A) ×( L/ E)              

∴          U = (½)P  × (PL/ AE) = P² L P /2 AE

If we rewrite above expression in terms of the stress ( P/A)  & the strain in the bar,

U = (½) × (P/ A) × (P / AE) × AL =( ½) × Stress × Strain × Volume

The strain energy per unit volume of the bar = (½) × Stress × Strain

=(1/2)  × σ × ε = σ²/2E           = E ε²/2

So, strain energy per unit volume of the material is as:

=          (Stress)/( 2 × Young's modulus)

 = (Young's modulus/2) × (Strain)²