Area by Simpson's Rule

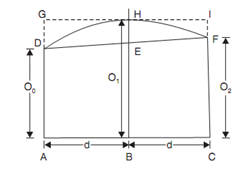
The boundary line between two segments is assumed parabolic in this method. In the shown figure the first two segments of figure, in which boundary between the ordinates is supposed parabolic.

∴          Area of the first two segments

= Area of trapezium ACFD + Area of parabola DEFH

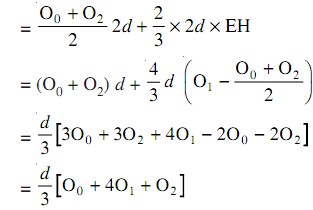
Area of next two segments

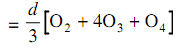
Area of last two segments

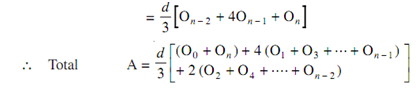
It is to be noted that the above equation is applicable if the number of segments (n) are even, otherwise, if total number of ordinates' are odd.

 If n is odd, by Simpson's rule then for n - 1 segments area is calculated and for the last segment trapezoidal rule is applied.

If the boundary is not irregular Trapezoidal rule gives better results to great extent. If the boundary is highly irregular Simpson's rule should be used. If the curve is concave towards the survey line this rule gives slightly more value compared to trapezoidal rule, and if the boundary is convex towards survey line gives lesser value.

if the number of segments is increased Accuracy can be improved In both of the methods.