Indeterminate Bars:

Along the reference to thermal stresses, bars whose thermal expansion is not restrained in particular  manner are known as determinate bars and the bars whose thermal expansion is restrained in any manner are called as indeterminate bars. As in the case of several of the other indeterminate problems thermal stress analysis of indeterminate bars might be carried out simply by the method of compatibility or consistent deformations.

Let the prismatic bar of length 'L' illustrated in Figure. The bar is associated to a rigid support at LHS and free at the other end. However at small distance 'd' from the free end of the bar there is a rigid body which would prevent any expansion of the bar beyond the small gap of which'd'. If the thermal expansion of the bar is less than or even equivalent to'd' no stresses shall be induced in the bar & the problem remains determinate. If the bar is heated furthermore, then temperature stresses shall be generated. As the bar is heated it shall push against the rigid support which shall restrain the expansion by exerting a compressive force on the bar, which should produce elastic shortening equal to the excess thermal expansion.

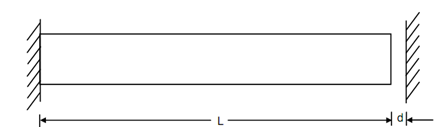
  Figure

Let us demonstrate the principle by a numerical instance. Let the length & cross-sectional area of the bar is 750 mm & 1200 mm2 respectively. Let us also supposed, d = 0.12 mm, E = 200 kN/mm², α = 12 × 10^{- 6} m/m/^oC and ΔT = 32^oC. By using the above data, we might readily compute the free thermal expansion of the bar is

             δ_t  = L × α × ΔT = 750 × 12 × 10^{- 6} × 32 = 0.288 mm

But this free expansion cannot take place because of the presence of the rigid restraint after a gap of 0.12 mm.

Supposing the elastic force in the bar as P, the elastic deformation δe might be calculated as

                                  δ _e  = PL/ AE

Any how the total deformation δ of the bar must be only equal to d. therefore; the compatibility condition might be expressed as

δ_t  + δ_e = d

(L × α× ΔT) + (PL / AE) = d

From which

P =- (L × α × ΔT - d ) (AE /L)

or         P =  α × (ΔT - (d /L))  AE

Putting the numerical values in Equation (18),

P =- (0.288 - 0.12) (1200 × 200)/750

= - 53.76 kN.

Now, stress induced σ _t = ( - 53.76 × 1000)/1200 = - 44.8 N/mm²

In several cases, the bar might already be kept between supports and'd' is zero so that we might write as follows :

P = α× ΔT × AE

or thermal stress            σ_t  = E × α × ΔT

Eq. implies that the thermal stress induced is a function of go up in temperature and elastic & thermal properties and not based on the geometric properties of the bar.