Visual realism:

Diffuse illumination alone does not give visual realism. With no angular dependence in the light, the observer will see no difference between a sphere and a disc.

For a perfect reflector, the entire incident light would be reflected back out in the direction of S. In fact, when the light strikes a surface it is scattered diffusely (i.e. in all directions) :

For an observer viewing at an angle (s) to the reflection direction S, some fraction of the reflected light is still visible (due to the fact that the surface isn't a perfect reflector - some degree of diffusion takes place). The amount of proportion of light visible is a function of the angle s (in fact it is proportional to cos (s)). It also depends on the quality of the surface and the angle of incidence i. We may define a coefficient w (i) - the specular reflection coefficient - that is a function of the material of which the surface is made and of i. Each surface shall have its own w (i).

Putting all this together gives following :

E_ss  = w (i) . cosⁿ (s) . I _s      

where,  E_ss is the intensity of the light ray in the direction of O,

      n is a fudge factor : n = 1 - rough surface (paper) n = 10 smooth surface (glass),

w (i) is generally never calculated - simply choose a constant (0.5?).        

In fact it is derived from the physical properties of the material from which the surface is made.

Eq. (2) contains the term cosⁿ (s). This is in fact fudge which has no basis in physics, but works to generates reasonable results. By raising cos (s) to the power n, what we do is control how much the reflected ray spreads out as it leaves the surface.

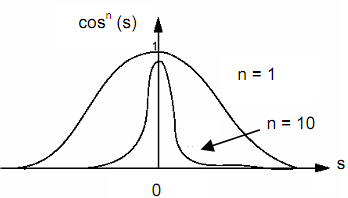
Figure: Controlling the Reflection - the Action of n