Pareto Optimal Allocations:
Definition:
An allocation x is Pareto optimal if it is feasible and there is no other feasible allocation that all consumers weakly prefer and at least one strictly prefers to x. Symbolically, a feasible allocation

Thus, it is impossible to make one agent better off without making other worse off. In the figure the indifference curves of A, B are tangent and at this point all gains trade are exhausted. This not always true however. If the preferences are not convex, then it is not true. Moreover, even in the case of strictly convex preferences, the set of Pareto optimal allocation may contain
other points, besides the options of tangencies of indifference curves. Essentially, therefore, we look for the set of tangency points of the indifference curves of A and B. The set forms the contact curve (CC) and the allocations that lie along this curve are Pareto efficient. Moreover, the set of choices of the agents agree to trade will lie somewhere on CC that passes through the lens defined by the points interior to uA and uB.
Example: (Due to Bar, M)
Find the Pareto optimal allocations of the following problem.
Solution:
You are given the description of a pure exchange economy with two agents (1 and 2); two goods (x,y) and initial endowment (o,oy). Solve for
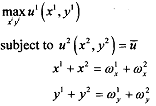
We want to maximise the utility of agent 1 when the utility of agent 2 is given. If we translate the problem to Pareto optimal formulation it is equivalent to saying that it is impossible to make agent 1 better off without making agent 2 worse off. The last two constraints of the problem give the feasibility constraints. To solve the problem substitute the feasibility constraints into the first constrain which produces the modified version of the problem as

The left hand side is the slope of agent 1 indifference curves (MRS1) and the right hand side is the slope of agent 2 indifference curves (MRS2). Thus, if we have "well behaved" preferences, we can find the set of Pareto optimal (PO) allocations using.
MRS1 = MRS2