William Gorman's Intransitivity Problem:

William Gorman demonstrated that while the Scitovsky double criteria rules out Scitovsky reversals, it does not rule out intransitive chains. For  instance, it may  be  that  an  allocation  G  is preferred  to allocation D,  allocation D  is preferred to allocation F but allocation F is not preferred to allocation G. This is shown in Figure, where there are three PPF_s (PPF_D,  PPF_F  and PPF_G) and three CIC_s corresponding to the Pareto-optimal allocations on each PPF (allocation D on CIC_D,  allpation F on PPF_F  and allocation G on PPF_G).  It can be  seen that unlike  in Figure, D  is superior to F by  the Scitovsky double criteria because  it  is better than F by  both  the Kaldor  and Hicks criteria and moreover, CIC_D  does not intersect PPF_F  while CIC_F  intersects PPF_D.

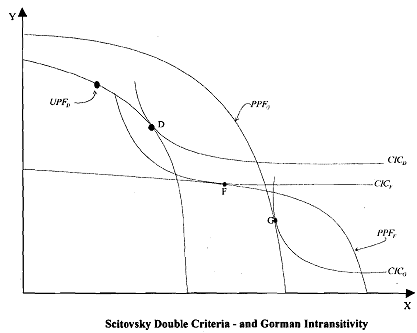
The problem of  intransitivity can now be visualized in Figure. As noted, by  the double criteria, D is preferred to F. By the same double criteria, it can be argued that G is preferred to D, as CIC_D  intersects PPFG  but CIC_G  does not. However, G and D do not  fulfill the double criteria, as CIC_F  intersects PPF_G and CIC_G  intersects PPF_F, a  situation similar to the one described in Figure.  Thus,  by  the Scitovsky double criteria,  G  is  preferred  to  D,  D  is preferred  to  F  but  G  is  not  preferred  to  F.  Consequently, although the Scitovsky double criteria  rules  out ranking  reversals and although G  is not preferred to F, F  is also not preferred to G and they are merely  incomparable, which implies that the ranking is intransitive.