Two-point transformation:

A two-point transformation is attained when two terms of the first three rows of the fourth column of the 4 × 4 transformation matrix are non-zero. For instance,

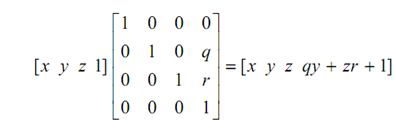
Two-point transformation contain two centre of projection and two vanishing points as in the above case centre of projections would be at

 [0,       -1/q , 0, 1 ]  and [0, 0, -1/r , 1]

To attain the two-point perspective transformation, two single-point perspective transformations are concatenated.

                                                [ p_qr ] = [ p_q ] [ p_r ]      

Likewise, if the initial three rows of the fourth column of the 4 × 4 transformation matrix are non-zero, three-point perspective transformation is attained.

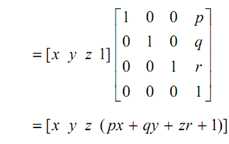
In this type of case, there are three centres of projections and three vanishing points.

However, Foley, et al. (in the year 1996) noted down that three-point perspectives are utilized infrequently since they offer little additional realism to two-point perspective projections.