Important Properties:

Many important properties of B-spline surfaces are listed here. These properties may be proved simply by applying the same techniques utilized for Bézier curves. Please compare these significant properties with those of B-spline curves. Please remember that the equation of a B-spline surface is the following

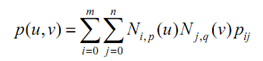
Here the degrees in the u- and v-directions are respectively p and q, and there are m + 1 rows & n + 1 columns of control points.

•          Non-negativity: N_i,p (u) N_j,q (v) is non-negative for all p, q, i, j and u and v in the range of 0 and 1.

This is obvious.

•          Partition of Unity : The addition of all N_i,p (u) N_j,q (v) is 1 for all u and v in the range of 0 and 1.

More exactly, it means for any pair of u and v in the range of 0 and 1, the following holds :

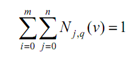
•             Strong Convex Hull Property: If (u, v) is in [u_i, u_{i + 1}) × [v_j, v_{j + 1}), then p (u, v) lies in the convex hull indicated by control points p_h,k, where i - p ≤ h ≤ i and j - q ≤ k ≤ j.

This strong convex hull property for B-spline surfaces directly follows from the strong convex hull property for B-spline curves. For the u-direction, if u is in [u_i, u_{i + 1}), then there are at most p + 1 non-zero basis functions, say, N_i,p (u), N_{i -  1,p} (u), . . . , and N_{i - p,p} (u). Therefore, only the control points on row i - p to row i have non-zero basis functions in the u-direction. Likewise, if v is in [v_j, v_{j + 1}), there are at most q + 1 non-zero basis functions on this knot span, namely N_j,q (v), N_{j - 1,q} (v), . . . , and N_{j - q,q} (v). Therefore, only the control points on column j - q to column j have non-zero basis functions in the v-direction. By combining these two facts together, just the control points in the range of row i - p to row i and column j - q to q have non-zero basis functions. As these basis functions are non-negative and their addition is one (that means, the partition of unity property), p (u, v) lies in the convex hull indicated by these control points.