Spring Subjected to Axial Couple:

Let us assume a close coiled helical spring subjected to a couple M illustrated in Figure (a). Two components can be asumed if α = angle of helix.

M_t = M cos α

T = M sin α

Out of these T → 0 as sin α → 0, as α is small. But Mt → M since cos α → 1. Therefore, the spring is subjected to a torque around axis, of magnitude M. The effect of M shall be to wind or unwind the coil of the spring, resulting into enhance or reduce in radius of the coil. This efficiently is the bending of the rod of the spring.

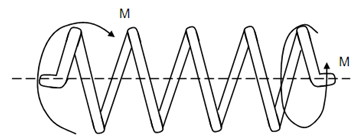
Figure

Let us say because of M working on the spring, the radius of the coil changes from R to R′. The

BM from theory of bending is specified by

M = EI ((1 / R′ )- (1/ R) )

This twisting of the spring (not the twisting of spring rod) or bending of the rod of the spring shall change the number of turns from n to n′ when length l shall remain same.

Note l = 2π n R = 2π n′ R′

∴          (1 / R′) -( 1 / R )= (2π/ l) (n′ - n)

Using (i) in Eq. (11) to find

M = 2π EI (n - n′) / l

You would remember that E = modulus elasticity of spring material and I = moment of inertia for rod section. The total twist in the rotation or spring

φ= 2π (n′ - n)

Therefore, from Eq.

φ= Ml /EI

or         φ=  M 2π n R/ E(π/4)d⁴ = 128 n M R   /Ed⁴

The rod of spring is subjected to BM

∴          Bending stress σ= 32 M / π d ³    

Strain energy in bending

 U = M ² l/2 EI = (1/2)             M φ

If U is divided through volume of the rod, the strain energy per unit volume.

u = σ²/8 E