Cyclic Neutron Activation Analysis (CNAA):

In case of elements with short- lived activation products, sensitivity is frequent hampered through low activity and thus reliability of the measurement is at stake. This difficulty is overcome by repeating the whole cycle of irradiation and counting several times and subsequently summing up the γ-ray spectra as typically illustrated in Figure.

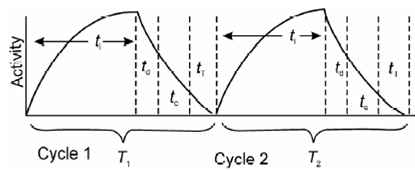
Figure: Schematic illustration of cyclic neutron activation analysis

Its primary theory has been developed and an equation derived for the total activity;

A=Nφσk/λ(1-e^-λti)( 1-e^-λtc)( e^-λtc)[(n/1-e^-λti)-(e^-λT)(1-e-^nλλ)/(1-e^-λT)²]  ...(13.16)

where A = total cumulative counts recorded in n cycles,

k = factor containing the detector efficiency and branching ratio for the decay path,

ti = irradiation time for each cycle,

tc = counting time for each irradiation,

td = delay time period to counting for each irradiation,

T= the delay period from the end of a previous delay period to the end of the next delay   period (cycle time, s), and

n = number of cycles.

Thus, having statistically significant counts, sensitivity is enhanced. A typical instance of this technique is the determination of aluminium using ²⁷Al(n, γ) ²⁸Al (t½ = 2.3 min) in bauxite using ²⁴¹Am-Be neutron source.