Simplified Theory - Elastic Critical Stress:

The allowable compressive bending stresses (σ_be) in a beam or girder is affected by the lateral bending of its thin components, which is taken care of by incorporating the factor elastic critical stress (f_cb) of the section, calculated by the following formula

 f_cb       = k₁ ( X + k₂ Y ) c₂/ c₁ in MPa

where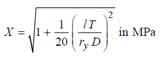

and Y= 26.5x10⁵/(1/r_y)² in MPa

Here, k₁ = A coefficient to allow for reduction in thickness (i.e. their curtailment) between points of effective lateral restraint and depends on the ratio, ψ

ψ = Ratio of whole area of both the flanges at the point of least BM to that at the point of greatest BM (values of k1, for different ψ values are given in IS: 800).

k₂ = A coefficient to allow for the inequality of flanges (unsymmetrical section) and depends on the ratio, ω, while

ω = Ratio of MI of compression flange alone/sum of the MI of the flanges, (the moments of inertia are calculated about its own axis parallel to the Y-Y axis of the girder at the point of maximum BM) (values of k₂ for different values of ω are given in IS : 800),

l = Effective length of compression flange

r_y = Radius of gyration about its axis of minimum strength (Y-Y axis),

D = Overall depth of beam,

T = Mean thickness of compression flange = Area of the horizontal portion of the flange ÷ width,

t = Web thickness,

d₁ = Depth of web (as defined below),

c1, c2 = Lesser and greater distances, correspondingly, from the neutral axis to the extreme fibres, and

I_y = MI of whole section about axis lying in plane of bending (Y-Y axis),

I_x = MI of whole section about axis normal to the plane of bending (X-X axis). Values of X and Y are given for appropriate D/T and l/r_y value in IS: 800.