State of Stress:
Instead, the state of stress at any point might be represented through a circle and a point on the circle represents the normal and shear stress components, on some plane as horizontal and vertical coordinates.
Now let us consider the circular representation more closely so as to obtain clear interpretation of the state of stress.
In Figure a coordinate system (σ, τ) has been formed with σ on horizontal axis and τ on the vertical downward axis. On this coordinate plane of σ - τ plane a point X is chosen whose coordinates are σx and τxy respectively. Also another point Y chosen with coordinates σy and τyx (or σy and - τxy).
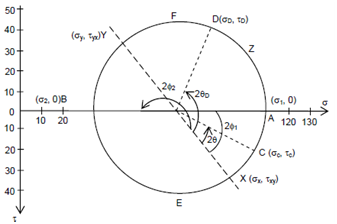
Figure: Circular Representation of State of Stress
These two points X and Y that represent the stress components on two planes and thus, according to Eq. (14), should be points on a circle. Point X represents x plane and point Y represents the y plane. While we join the points X and Y by a straight line, we search that the line passes by the point O¯ on the σ axis which should be the origin of the circle described by Eq. (14). As O¯ is the origin of circle X and Y are points on the periphery of the circle the line X O¯ Y (or simply XY) should be the diameter of the circle which we are trying to establish. Therefore, draw a circle along with XY as diameter.
Now any point of this circle should represent the state of stress on an oblique plane. Let us suppose a few specific points. Points A and B lie on the horizontal (σ) axis, i.e. τ = 0 and hence they represent the two principal planes. Because σ is maximum at A, point A represents the main principal plane (and hence, σ coordinator of A is σ1) and point B represents the minor principal plane. ∠ XO¯A and ∠ XO¯B are equal to 2θ1 and 2θ2 respectively where Φ1 and Φ2 are the inclinations of the major and minor principal planes with the x plane.
Consider any arbitrary point say C such that the angle ∠ XO¯C is equal to 2θc. Then, the coordinates of the point C give the normal and shear stress components on plane inclined at θc to the x plane. Same, Every point Z on this circle might be interpreted to provide the normal and shear stress components on a plane whose inclination with x axis is 1/2 ∠ XO¯Z.