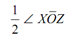Interpretation of the state of stress:

Now let us consider the circular representation more nearly so as to get clear interpretation of the state of stress.

In Figure a coordinate system (s, t) has been formed with s on horizontal axis and t on the vertical downward axis. On this coordinate plane of s - t plane a point X is chosen whose coordinates are s_x and t_xy respectively. Also another point Y chosen with coordinates s_y and t_yx (or s_y and - t _xy).

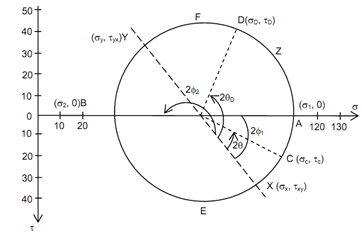
                             Figure: Circular Representation of State of Stress

These two points X & Y represent the stress components on two planes and therefore, according to Eq. must be points on a circle. Point X show x plane & point Y represents the y plane. While we join the points X & Y by a straight line, we discover that the line passes through the point O  on the s axis which must be the origin of the circle defined by Eq. As O is the origin of circle X and Y are points on the periphery of the circle the line  (or simply XY) should be the diameter of the circle which we are trying to establish. therefore, draw a circle with XY as diameter.

Now any particular point of this circle must represent the state of stress on an oblique plane. Let us assume a few particular points. Points A and B lie on the horizontal (s) axis, i.e. t = 0 and therefore they represent the two principal planes. Since s is maximum at A, point A represents the major principal plane (and therefore, s coordinator of A is s₁) and point B shows the minor principal plane.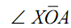 and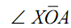 are equal to 2q₁  and 2q₂ respectively where f₁  and  f₂ are the inclinations of the major and minor principal planes with the x plane.

Let any arbitrary point say C such that the angle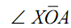 is equal to 2q_c . Then, the coordinates of the point C specified the normal & shear stress components on plane inclined at q_c  to the x plane. Likewise, each of point Z on this circle might be interpreted to give the normal and shear stress components on a plane whose inclination with x axis is