Dividing a Circle into Three, Six and Twelve Equal Parts:

The component shown in diagram (a) has three equal-spaced holes. The circle must be divided into three equal parts. This can be done by means of a compass in diagram (b). From A as the center and with the radius equal to that of the given circle draw an arc which will intersect the given circle, at points 2 and 3. Points 1, 2 and 3 divide the circle into three equal parts. The same can be obtained by making use of a 30^o-60^o triangle, as shown in diagram(c).

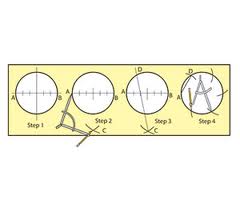
The component shown in diagram (a) has six equal-spaced recesses and six holes. Here we have to divide a circle into six equal parts. Here we apply the same method as in diagram, the only difference being that two arcs are described from points 1 and 4 as the centers in diagram (b). The identical result can be obtained by making use of a 30^o-60^o triangle diagram (c). Make sure that the dividing lines pass through the center of the circle. To divide a circle into 12 equal parts first we divide the circle, as declared above, into six equal parts as shown in diagram (b) or (c).

Then divide the circle into 12 equal parts via making use of 30^o-60^o triangle against a ruler, as indicated in diagram, through dot and dash lines.