Preferences Over Lotteries:

While we need to choose among lotteries, there is no obvious way  to do this. In  the  process of making a choice, however,  it  looks reasonable  to assume, you will be able to express a preference over any pair of lotteries. The  basic premise  of modelling preference  is that  you  care only about the reduced lottery over final outcomes. Hence, you will be effectively indifferent to the compound lotteries underlying those reduced lotteries. Let  there  be  a set  of  lotteries 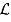from which  a choice  is  to  be  made.  We assume that consumer has a preference relati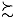on on 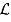 . That is, if we select two lotteries, L and  L'  from space 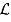and write

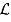
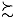L'  implying thereby L is at  least  as  good  as  lottery L.  If  such preferences have the properties  of completeness, reflexivity and transitivity,  the individual would be able to rank her preferences. Recall that these concepts have been discussed in consumer's preference theory with certainty. But if you  like, we will assume that 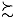are such that  

• for all x and y in X  either x 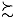y or y  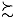 x or both (completeness)
• 1.x+O.y ∼ x  (reflexive)
• for all x, y and z in X,

if x 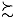y and y 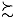z, then x  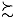 z (transitivity)

In the above, completeness indicates that the individual can compare any two lotteries, while transitivity means,  if one lottery is at least as good as another, which in turn, is at least as good as  the third, then this individual will rank the first lottery as being at least as good as the third. Along  with the rationality  of  preferences  k,  let  us  bring  in  an additional regularity  assumption  ("continuity")  to rule out certain discontinuous behaviour. Broadly,  the  continuity  axiom says that  small  changes in probabilities do not change the nature of the ordering of two lotteries.