St. Petersburg Paradox:

A coin is flipped until  a head  appears on the n^th flip, at which  the player  is paid Rs. 2".  If X_i  represents the prize awarded when the first head turns up on the ith  trial, then  

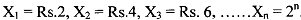
The probability of getting a head  for the first time on the i ^th trial,  is  (1/2)'.  see that it is the probability of getting (i  - 1) tails and  then a head. Hence,  the probabilities of prizes, Π_i are

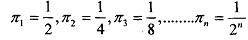
the expected value of the game is

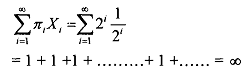
Since the expected value of the game is m, how much would you be willing to pay to play this game? Perhaps, not more than a few rupees. Thus, the game in this sense not worth its large expected value (no taker to enter  it). As a solution to this paradox, it was argued that individuals attached negative 'utility value' to  expected 'monetary value'. Because utility may  rise less rapidly than the monetary value of the prizes, the utility value of the game will  fall short of its monetary value. Thus, uncertain prospects are worth less in utility terms than certain ones, even when expected tangible payoffs are the same.