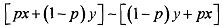Expected utility theory:

When  the preference relations and  continuity  assumptions are  satisfied, we can conclude that there exists a utility function

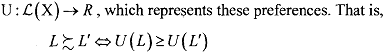
For making this formulation workable, we need to take expectation of utilities. Before  doing that,  it will  be  useful  to examine lotteries without uncertainty (or, sure winning lotteries). Let lotteries

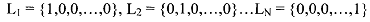
give 'no uncertainty7 representation. Then it is not unreasonable to view utility of such a lottery as simply utility of having the corresponding state for sure. So we  can write u(x_k) = U(L_k). But it  is  generally not  true  that  utility  of  a lottery  is equal  to  the  expected utility  of  the  states given the probability distribution of the lottery.  

Independence Axiom:

The  preference relation 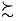on  the space of  simple lotteries 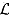statistics the independence axiom if for all

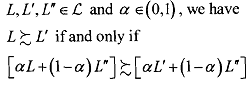
We interpret the above preference relation in words as follows:

When we mix each  of  two lotteries with  a third one, then the preference ordering of the two resulting mixtures does not depend on, or independent of, the particular third lottery used. To see more specifically, suppose you choose L while comparing L and  Lf  .  Next suppose that, whether you choose L or  Lf with some probability  (1 -a),  you  will  be  facing a different lottery  L"  . Independence axiom says,  this  additional uncertainty  which  is  the  same whatever your choice is, should not matter for your choice. Therefore, this axiom also says,  the  order (or frame) of lotteries  is unimportant. That is,