Third model model of Chamberlin:

Chamberlin argued that in practice  equilibrium is achieved by price adjustments of existing firms as well as new entry. Equilibrium is stable if the dd´ is tangent to the average cost curve and expected sales are equal to the actuals (i.e., the dd' curve cuts the DD´ at the point of tangency of dd´ and LAC). We start with the point e1 (see Figure), where there is abnormal profit. New firms are alternated until D₁D₁´ shifts to D₃D₃´. Some might take e2 as a long run equilibrium with (P, X) price output combination since only normal profit is earned these. However, this is not true. Each firm believes d₁d₁ is its demand curve and if prices are lowered, output sold goes up and hence profit will increase. However, each firm having the same incentive to reduce price. As a result, dd' slides down and each firm realises a loss instead of profit.

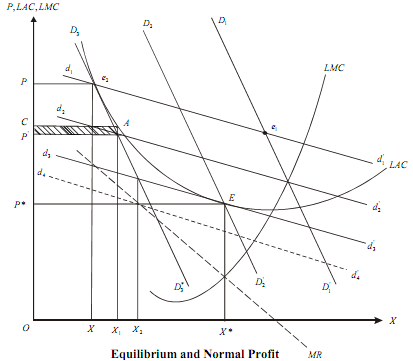
For example, see that at position d₂d₂´. The firm has reduced price to P´ but others have not done similarly and X₁ is produced with a total loss equal to the shaded area CP'BA. Each firm still believes that it can achieve positive profit by cutting price. The loss infact increases further as d₂d₂´ slides down along D₁D₁´. The process would end when dd´ becomes tangent to the LAC. This will happen if the firms produce X*. However, still there are too many firms and their share is X₂ (given by intersection of D₃D₃´ and d₃d₃´). Firms in order to achieve X* (to maximize profit since at X*, MR=MC) reduce price. As a result, d₃d₃ slides down further to the left and with increasing losses. The firms, which cannot bear this loss, quit D₃D₃' and move to the right to D₂D₂.

Exit will continue till d₃d₃' becomes tangent to LAC, and D₂D₂´ cuts d₃d₃´ at the point of tangency. The point E is the table equilibrium where (p*, X*) is the equilibrium price quantity combination. Firms earn normal profit and no entry or exit takes place.