Centroid of Thin Wires:

A thin uniform wire bent in a specified shape ABCDE (lying in one plane, XOY) may be divided into a appropriate number of straight lengths for each of which its centroid is known to be at its mid-point.

 [Note : 'O' is any arbitrary Origin of Axes in Plane XOY.]

If wire of entire length L is formed of L₁ = AB, L₂ = BC and so on, with their mass-centres (or C. G.) situated at their mid-points G₁, G₂ etc., then L =  L₁ +  L₂  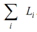+ ... =   . You may apply Varignon's theorem again as follows :

Let that the plane XOY is horizontal so that axes OX and OY both lie in it and are horizontal. Supposing the weight of wire as w Newtons/metre length, we have following :

 Weight of portion,         AB = wL₁ = W₁

Weight of portion,          BC = wL₂  = W₂ , and so on

Total Weight,                  W = W₁ + W₂  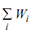+ ... =    = w ∑ L_i

Letting first moment of all of these weights about axis OY, if the overall mass-centre, we have :

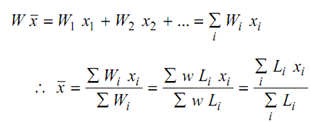
Likewise, considering first moment of weights about y axis

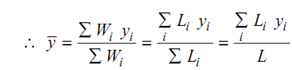
 [Note : Similar to C. G. of  a thin uniform wire, the concept of centroid of length may be defined. Therefore, the above referred point (x, y) may be said to be the centroid of length ABCDE.]

For irregularly shapes wires, while term L₁, L₂ etc. occurring in the above expressions become infinitesimally small, the expressions for x¯ and y¯ may be written as,

x¯ =∫ x dL / ∫ dL

y¯ =  ∫ y dL / ∫dL

Here, dL is the length of differential element and (x, y) is the coordinates of its centroid.