Product of Inertia:

Product of Inertia of typical channel section around centroidal axes CX and CY is significant property of a given section. These are the principal axes although the channel section is symmetrical only about one axis CX.

By definition, product of inertia about X and Y axes,

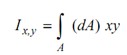
We determine that for a symmetrical section illustrated in Figure, for any element P of area dA and co-ordinates (x, y), there is an element P′ of same area dA with co-ordinates (x, - y).

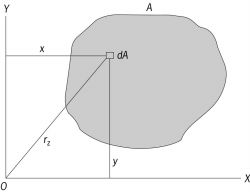
Therefore, the products of inertia for these two elements are equivalent and opposite, and for these may write:

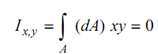
The product of inertia of areas which do not have any axis of symmetry are non-zero. Also, the product of inertia for the symmetrical channel section exists with respect to any other rotated axes Y ′Y ′ as illustrated in Figure.