Group Technology Coding System
Too much information about the components sometimes makes the decision very hard proposition. It would be better to provide a system along with an abstract kind of thing, which might summarize the entire system with the necessary information without giving great details.
GT is a fitting tool for this reason. Coding, a GT technique, might be used to model a component with essential information. While constructing a coding system for a component's representation, there are various factors need to be let. They include
- The population of components (i.e., prismatic, rotational, deep drawn, sheet metal, and so on)
- Detail in the code.
- The code structure.
- The digital representation (i.e. binary, decimal, octal, alphanumeric, hexadecimal, and so on).
In component coding, only those features are included that is variants in nature. While a coding scheme is designed, the two criteria ought to be fulfilled (A) unambiguity, and (B) completeness.
We might define coding as a function of F that maps components from a population space P into a coded space C . Unambiguity of a code might be defined (for component j) as :
j P = ∃ only once i C = i = F (j) . . . (1)
Completeness might be defined as
∀ j P ∃ i C = i = F (j) . . . (2)
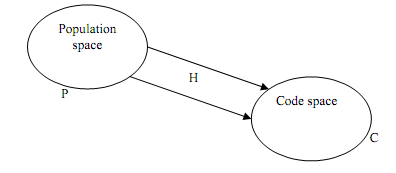
Figure: Mapping from a Population Space to a Code Space
The two properties recommend that each of components in a population has its own unique code. Although, if two codes are complete & unambiguous, the one having more conciseness is opted while a longer code is normally essential whenever more detail is required, for example in basic Opitz code system and the KK-3, former one uses 5 digits to explained the shape of the component. 5 digits might represent 105 combinations. With this set, this is quite difficult to show all the details of a component. Thus, KK-3 of Japan (Japan Society, 1980), which has 21 digits & contains multiple digits for single feature, and MICLASS of TNO (Houtzeel & Schilperoort, 1976), which contain a 12-digit code, is utilized.