Proof of Castiglianos Theorem:

Mathematically if the total strain energy, U, refer to a function of the loads

Pi (i = 1 to n), then

δ_m  = ∂U / ∂Pm

here δ_m is the displacement of the point of application of the load Pi in the direction of P_m.

Let us prove the theorem now. Assume the beam in Figure 9 with forces P_A, P_B, P_C, etc. working at points A, B, C, etc.

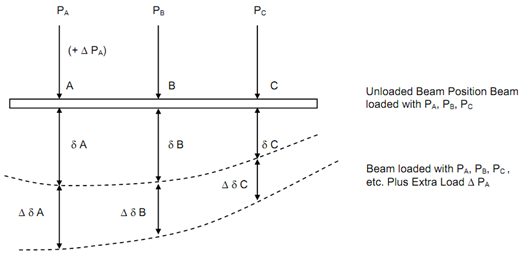
Figure

Let δ_A, δ_B, δ_C, etc. be the deflections in the direction of loads at the points A, B, C, . . ., respectively.

After that, the strain energy of the system is equivalent to the work done.

U = (½) P_A δ A+ (½) P_B δ_B   +( ½) P_C δ_C       + .. .

If one of the loads P_A is now enhanced by an amount Δ P_A, the changes in the deflection shall be Δ δ_A, Δ δ_B, Δ δ_C, etc. as illustrated in Figure. In enhancing the load from P_A to

(P_A + Δ P_A), extra work is completed and it is as follows .

Extra work done at A =  P_A + (½) Δ P  × Δ δ_A

Extra work done at B = P_B  × Δ δ_B

Extra work done at C = P_C  × Δ δ_C

Likewise, in the case of other load also. After that, the total extra work one,

 = P_A  Δ δ_A   + 1 Δ P_B Δ δ_B   + P_B Δ δ_B   + P_CΔ δ_C      + ...

This must be equal to enhances in strain energy Δ U.

By Neglecting the product of small quantities (Δ P_A Δ δ_A) As they are very small as compared to the other terms.

ΔU = P_A  Δ δ _A  + P_B  Δ δ_B  + P_C  Δ δ_C  + .. .