Application of Castiglianos theorem:

Let us now consider the case where we apply the loads (PA + Δ PA), PB, PC, etc. gradually to the full value. As the ultimate loads in the case are exactly the similar as the earlier case and as all of the loads are applied statically, the ultimate deflections must also be the same. After that, the strain energy in the case, U′ (by neglecting product of small terms Δ PA Δ δA) would be as follows:

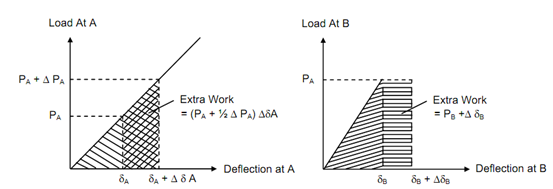
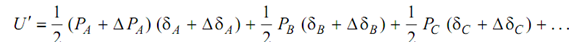
U ′ = (½) (P_A + Δ P_A ) (δ_A   + Δ δ_A) + (½) P_B(δ_B   + Δ δ_B) + (½) P_C (δ_C + Δ δ_C ) + ...

= (½) P_A  δ _A  + (½) P_A  Δ δ_A   + (½) Δ P_A  δ_A   + (½) P_B  δ_B   + (½) P _B Δ δ_B + (½) P_C δ _C+ (½) P_C Δ δ_C + ...

= 1 P _Aδ_A   + 1 P_B δ_B   + 1 P_C δ_C + .. . + 1 P_A Δ δ_A   + 1 P_B  Δ δ_B + 1 P _CΔδ_C + .. . + 1 Δ P_A  δ_A

= U + 1 P_A Δδ_A  + 1 P_BΔ δ_B   + 1 P _CΔδ_C        + ... + 1 P_A  δ_A

Though, since loads in addition to deflections are the similar in both the cases, the total strain energy must also be the same. Hence,

U ′ = U + ΔU

or         ΔU = 1 P_A Δδ  _A+ 1 P_B Δδ_B  + 1 P_C Δδ_C          + .. . + 1 Δ P_A  δ_A

∴          2ΔU = P_A  Δδ _A  + P_B  Δδ_B + P_C  Δ δ_C  + ... + Δ P_A  δ _A

Earlier we have achieved

ΔU = P_A  Δ δ _A  + P_B  Δ δ_B  + P_C  Δ δ_C  + .. .

Now, from the last two expressions, we get

ΔU = Δ P_A  δ_A  or ΔU / Δ P_A  = δ_A

In the limit, δ_A   = ∂U / ∂P_A

Likewise, it can be shown that ∂U /∂PB = δ_B , ∂U/ ∂PC = δ_C , etc.

Thus, in general, ∂U /∂PM = δ_M .

As a simple instance of the application of Castigliano's theorem, let us assume a bar of cross-sectional area A & length L under axial tension P. From previous section we have known that the strain energy U in this case is given as

U = P² L /2 AE

If we differentiate U with P, we get,

∂U /∂P = PL/ AE

That we identify as the extension of the bar under the load P that is the displacement of the point of application of load P.