Mathematical Representation of Cartel Equilibrium:

Supposing there are two firms in the market, joint profit maximisation implies that the firms maximise their respective profits i.e., maximise Π = Δ₁ + Δ₂.

Let P = f(X) = f(X₁ + X₂) be the demand function and
C₁ = f₁(X₁) and C₂ = f₂ (X₂) be the cost functions of the two firms. Then,
Δ₁ = R₁ - C₁ and Δ₂ = R₂ - C₂.
Therefore, Δ = Δ₁ + Δ₂ = R₁ - C₁ + R₂ - C₂  = R - C₁ - C₂  

The first order condition for profit maximisation requires that we differentiate Δ with respect to X₁  and X₂  separately and set the derivatives equal to zero. So,

∂Δ/∂X₁ = ∂R/∂X₁ - ∂C₁/∂X₁= 0 and

∂Δ/∂X₂ = ∂R/∂X₂ - ∂C₂/∂X₂= 0

From the above equations, the optimality condition is,

MR = MC₁ = MC₂

That is, at the optimum, the marginal costs from each plant must be equal and such equality should again be equal to the marginal revenue. Otherwise, the firms would still have some incentive to reshuffle the level of output production from each plant.

The second order condition for joint profit maximisation requires that,

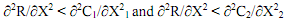
This implies that for each plant, it should be such that once the profit maximising output level has been reached, any additional unit of output would have the MR falling at a faster rate than MC.