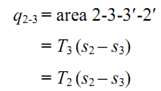Isentropic Compression Process:

The air is compressed isentropically as indicated by the curve 1-2 on p-v & T-s diagrams. Throughout this process, the pressure of air increases from p₁ to p₂, particular volume diminishes from v₁ to v₂ & temperature enhance from T₁ to T₂. We know that throughout isentropic compression, no heat is absorbed or discarded by the air.

Isothermal Compression Process:

Now the air is compressed isothermally (that is at constant temperature, T₂ = T₃) as indicated by the curve 2-3 on p-v & T-s diagrams. Throughout this procedure, the pressure of air increases from p₂ to p₃ and particular volume decreases from v₂ to v₃. We know that the heat discarded by the air throughout isothermal compression per kg of air,