Reactance and frequency:

In several ways capacitive reactance behaves like a mirror image of the inductive reactance. But, X_C is an extension of X_L into negative values which are below zero.

If frequency of an alternating current source can be given in hertz as f and the capacitance of a capacitor in farads as C, then capacitive reactance can be given by

X_C = 1/(6.28fC)

This same formula applies if frequency, f, is in megahertz and capacitance, C, is in microfarads (µF). Keep in mind that that if the frequency is in millions, the capacitance should be in millionths.

Capacitive reactance varies inversely with frequency. This means that the function X_C vs f appears as the curve when graphed, and this curve blows up as the frequency around zero.

Capacitive reactance varies inversely with actual value of capacitance, given a fixed frequency. Thus, the function of X_C vs C also appears as a curve which blows up as the capacitance nearly approaches zero.

The negative of Xc is inversely proportional to the frequency, and also to capacitance. Relative graphs of these functions are shown in the Figure given below.

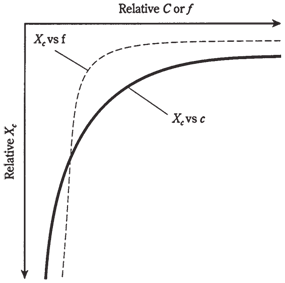
Figure--   Capacitive reactance is negatively, and inversely, proportional to frequency (f) and to capacitance (C).

Problem :

A capacitor has the value of 0.00100 µF at the frequency of 1.00 MHz. What do you mean by capacitive reactance?

Use formula and plug in the numbers. You can do this directly, as the data is specified in microfarads and in megahertz:

X_C =- 1/(6.28 * 1.0 * 0.00100) = -1/(0.00628) =- 159 Ω

This is rounded to 3 significant figures, as all the data is given to this many digits.